Na pierwszy rzut oka może się wydawać, że do oceny inwestycji wystarczy wiedzieć, ile pieniędzy finalnie zarobiliśmy. W końcu jeśli kapitał wzrósł o 40% albo 60%, brzmi to bardzo dobrze? Problem polega jednak na tym, że sama łączna stopa zwrotu niewiele mówi o tym, jak efektywnie nasze pieniądze pracowały w czasie. A to właśnie czas jest w inwestowaniu jednym z kluczowych czynników.
Średnioroczna stopa zwrotu porządkuje ten pozorny chaos. Sprowadza wyniki inwestycji do wspólnego mianownika, pokazując rzeczywiste tempo wzrostu kapitału w ujęciu rocznym, z uwzględnieniem procentu składanego. Dzięki temu inwestycje trwające różną liczbę lat można porównywać w sposób uczciwy i zrozumiały.
Średnioroczna stopa zwrotu to miara, która pokazuje przeciętne tempo wzrostu inwestycji w skali jednego roku, przy założeniu, że zyski są na bieżąco reinwestowane. Innymi słowy, odpowiada ona na pytanie, z jaką „prędkością” rosły nasze pieniądze w czasie — niezależnie od tego, jak długo trwała dana inwestycja. Jest to jedno z podstawowych narzędzi wykorzystywanych do analizy wyników w długoterminowym inwestowaniu.
Ma to szczególne znaczenie wtedy, gdy zastanawiamy się nad wyborem strategii inwestycyjnej. Bez średniorocznej stopy zwrotu łatwo ulec złudzeniu, że dana inwestycja była „lepsza” wyłącznie dlatego, że przyniosła wysoki łączny zysk — mimo że trwała znacznie dłużej niż inne dostępne alternatywy. Annualizacja wyników pozwala szybko zweryfikować, czy wysoki zysk był efektem trafnej strategii, czy jedynie konsekwencją długiego horyzontu czasowego.
Średnioroczna stopa zwrotu jest również niezwykle pomocna przy porównywaniu inwestycji z innymi formami lokowania kapitału — takimi jak lokaty bankowe, obligacje czy szerokie indeksy giełdowe. Dopiero analiza wyników w ujęciu rocznym pozwala realnie ocenić, czy podjęte ryzyko miało sens i czy nasze pieniądze mogły pracować efektywniej w innym miejscu.
Krótko mówiąc, średnioroczna stopa zwrotu pomaga inwestorowi spojrzeć na wyniki z dystansu — bez emocji i bez mylących skrótów myślowych.
Jak policzyć średnioroczna stopa zwrotu (CAGR)
Najlepiej wyjaśnić to na prostym przykładzie. Załóżmy, że zainwestowaliśmy kwotę 10 000 PLN, a po 5 latach wartość tej inwestycji wzrosła do 15 000 PLN. Oznacza to, że całkowita stopa zwrotu wyniosła 50%.
Aby jednak obliczyć średnioroczną stopę zwrotu, nie wystarczy po prostu podzielić 50% przez 5. Taki wynik byłby błędny, ponieważ nie uwzględnia faktu, że już wypracowane zyski są reinwestowane, czyli działania tzw. procentu składanego.
Aby poprawnie policzyć średnioroczną stopę zwrotu, należy skorzystać z odpowiedniej formuły matematycznej:
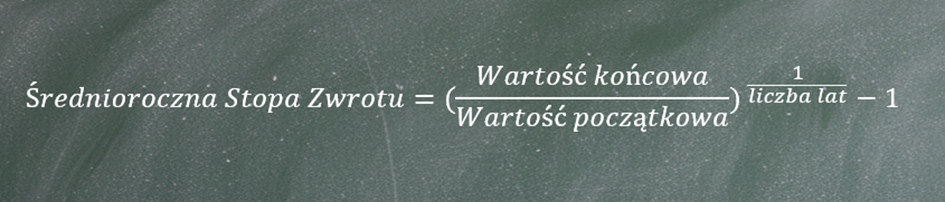
Ten sam wynik można zapisać również za pomocą pierwiastka stopnia n z ilorazu wartości końcowej i początkowej inwestycji, pomniejszonego o 1, gdzie n oznacza liczbę lat trwania inwestycji.
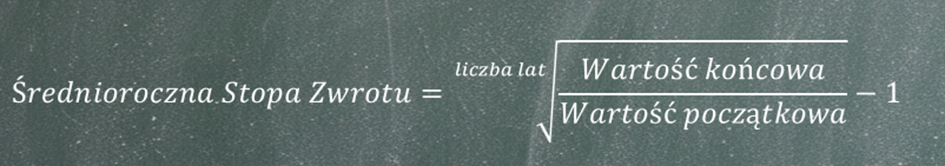
W różnych źródłach finansowych, blogach czy zestawieniach bardzo często spotyka się anglojęzyczny skrót CAGR (Compound Annual Growth Rate). Jest to dokładnie to samo pojęcie, czyli średnioroczna stopa zwrotu. Policzmy więc CAGR dla naszego przykładu. Dysponujemy wszystkimi potrzebnymi danymi: wartością początkową inwestycji, wartością końcową oraz liczbą lat jej trwania.
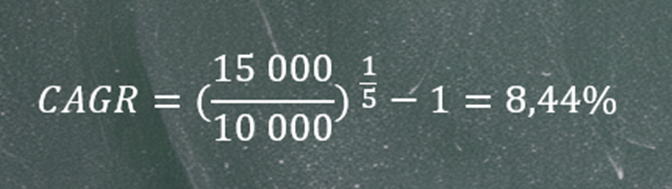
Aby osiągnąć 50% całkowitej stopy zwrotu w okresie 5 lat, należało uzyskiwać średnią stopę zwrotu na poziomie 8,44% rocznie. Jest to wyraźnie mniej niż 10%, które wynikałoby z prostego podzielenia 50% przez 5.
W praktyce nie zawsze mamy do czynienia z pełnymi latami inwestycji. Czasami inwestycja trwa kilkanaście miesięcy lub znacząco krócej niż rok. W takich przypadkach wystarczy dokonać niewielkiej korekty we wzorze i zamiast lat użyć liczby dni. Całość sprowadza się jedynie do zachowania odpowiednich proporcji.

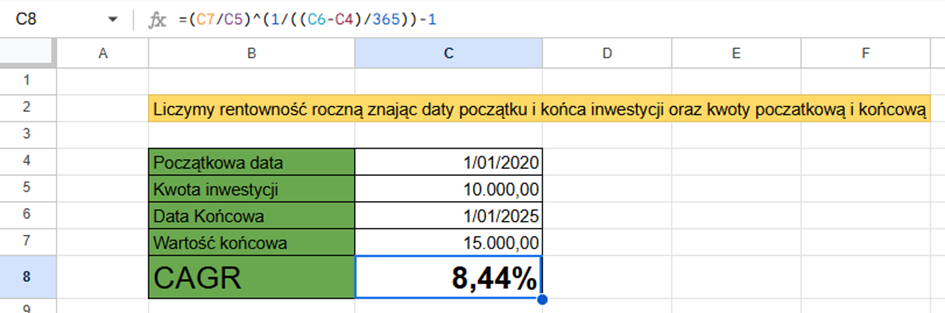
W praktyce nie ma jednak większego sensu liczyć tego ręcznie. Do tego celu idealnie nadają się Excel oraz Arkusze Google.
Stopa zwrotu ważona kapitałem ( MWRR)
Dotychczasowy przykład był stosunkowo prosty. Kapitał został wpłacony na początku inwestycji, a następnie osiągaliśmy różne stopy zwrotu w kolejnych latach, by na końcu obliczyć średnią stopę zwrotu za cały okres, czyli liczyliśmy klasyczną średnią geometryczną.
Rzeczywistość inwestycyjna bywa jednak znacznie bardziej złożona. W praktyce inwestujemy różne kwoty w różnych momentach czasu, a dodatkowo mogą pojawiać się wypłaty środków. W takiej sytuacji naturalnie pojawia się pytanie, jak poprawnie obliczyć rzeczywistą stopę zwrotu. Im więcej wpłat i wypłat, tym bardziej problem staje się skomplikowany.
Istnieją dwa główne podejścia do tego zagadnienia. Pierwszym jest stopa zwrotu ważona kapitałem — MWRR (Money-Weighted Rate of Return), a drugim stopa zwrotu ważona czasem — TWRR (Time-Weighted Rate of Return). W tym artykule skupiam się na MWRR, ponieważ lepiej odzwierciedla ona sytuację indywidualnych inwestorów, którzy samodzielnie decydują o terminach i wysokości wpłat.
TWRR jest natomiast bardzo dobrą miarą do oceny efektywności zarządzających aktywami, którzy nie mają wpływu na przepływy środków do i z funduszy.
Skupmy się jednak na MWRR. Jeżeli nie prowadzisz funduszu inwestycyjnego, jest to najwłaściwsza stopa zwrotu do analizy własnych wyników. W praktyce najlepszym sposobem na jej obliczenie jest skorzystanie z Excela lub Arkuszy Google, jednak dla pełnego zrozumienia warto najpierw przyjrzeć się matematycznym podstawom tego wskaźnika.
Obliczanie MWRR polega na znalezieniu jednej stopy procentowej, która — przy uwzględnieniu wszystkich historycznych wpłat i wypłat — prowadzi do uzyskania końcowej wartości kapitału.
Przykład
Załóżmy, że przez 3 lata inwestujemy po 12 000 rocznie. W pierwszym roku osiągamy stopę zwrotu na poziomie 10%, w drugim 15%, a w trzecim 20%.
Intuicyjnie mogłoby się wydawać, że średnia stopa zwrotu wynosi 15%. W rzeczywistości jednak tak nie jest, ponieważ w latach, w których osiągaliśmy wyższe stopy zwrotu, pracował już większy kapitał. Nie zadziała tutaj ani średnia arytmetyczna ani geometryczna, a powodem są dodatkowe wpłaty.
Najpierw policzmy końcową wartość inwestycji.
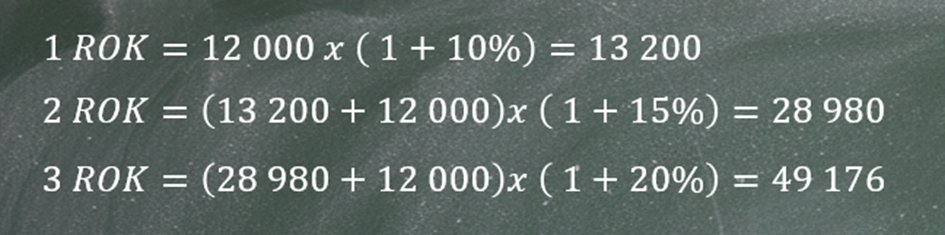
Następnie musimy znaleźć jedną średnią stopę zwrotu dla całego okresu. Zamiast używać trzech różnych wartości — 10%, 15% i 20% — szukamy jednej stopy, która przy takich samych wpłatach (12 000 rocznie) pozwoli uzyskać końcową kwotę 49 176.
W tym celu każdą wpłatę traktujemy oddzielnie i inwestujemy ją przez odpowiedni czas z tą samą stopą zwrotu.
Pierwsze 12 000 pracowało przez 3 lata, drugie 12 000 przez 2 lata, a ostatnie 12 000 przez 1 rok,
Suma wszystkich tych inwestycji powinna dać 49 176 zł.
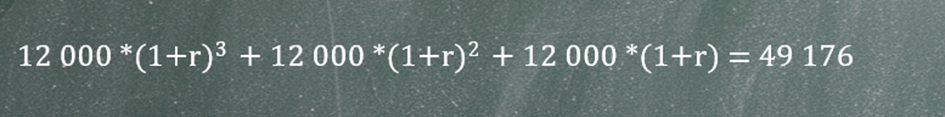
Z obliczeń wychodzi, że r = 16,43%.
Równanie to można łatwo przekształcić do postaci:
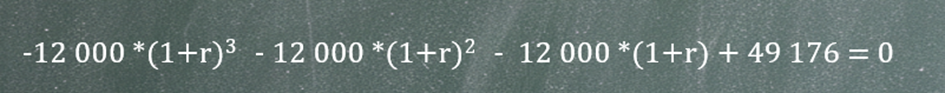
i z tego zapisu przejdziemy płynnie do ogólnego wzoru matematycznego
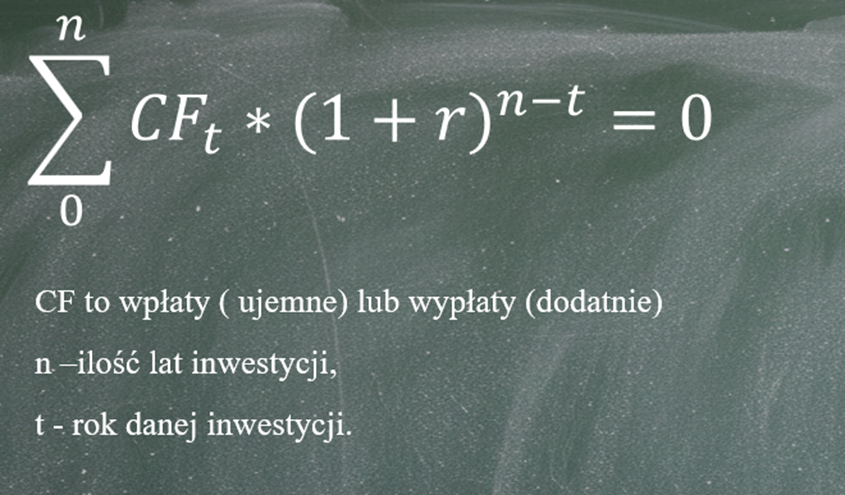
Ten sam przykład można zapisać również w równoważnej postaci, dzieląc obie strony równania przez (1+r)3
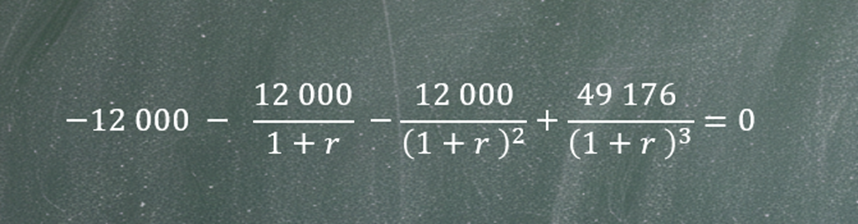
I z tego zapisu dojdziemy do wzoru, który jest dużo bardziej popularny.
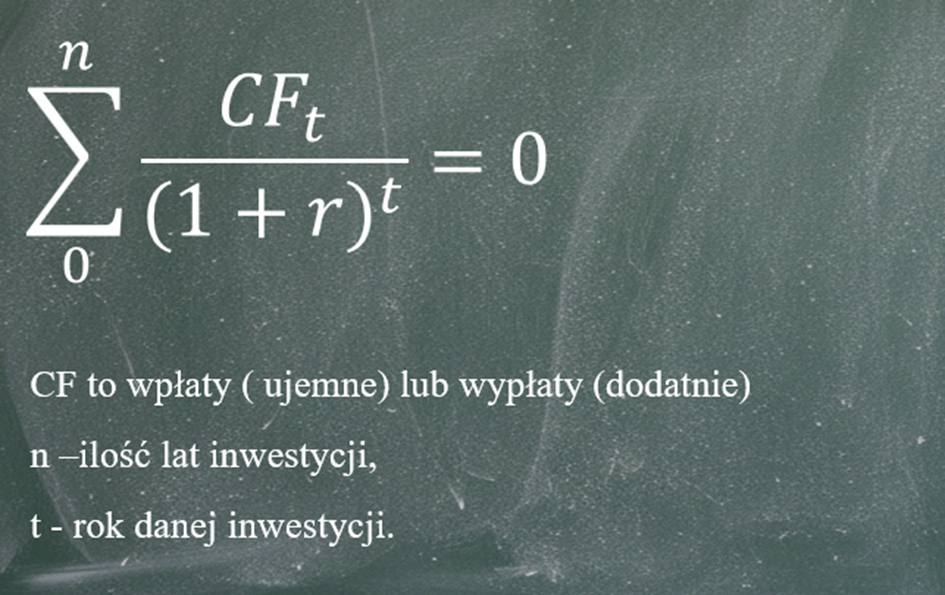
I z tym wzorem pewnie spotkacie się częściej. Oba równania dają jednak ten sam wynik.
W praktyce jednak nikt nie liczy tego ręcznie. Do tego celu służy Excel. Zarówno w Excelu, jak i w Arkuszach Google funkcją służącą do obliczania MWRR jest XIRR, gdzie najpierw podaje się wartości przepływów pieniężnych, a następnie odpowiadające im daty.
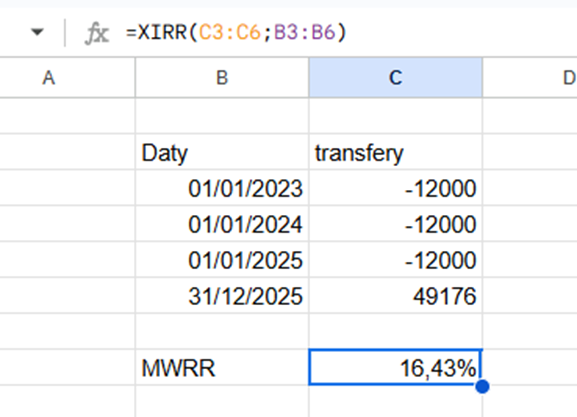
Podsumowanie
Średnioroczna stopa zwrotu CAGR oraz stopa zwrotu ważona kapitałem MWRR to niezwykle przydatne narzędzia, które pozwalają inwestorowi lepiej zrozumieć, jak w rzeczywistości pracuje jego kapitał. CAGR sprawdza się idealnie w prostych inwestycjach z jedną wpłatą, natomiast MWRR staje się nieoceniona w realnych scenariuszach, w których występuje wiele wpłat i wypłat w różnych momentach czasu.
Dzięki tym wskaźnikom możemy nie tylko rzetelnie ocenić skuteczność inwestycji, lecz także porównywać różne strategie i produkty finansowe w sposób uczciwy, uwzględniający zarówno czas, jak i skalę zaangażowanego kapitału. Umiejętność obliczania i interpretowania średniorocznej stopy zwrotu daje inwestorowi realną przewagę w podejmowaniu świadomych decyzji, pomaga unikać pułapek intuicyjnych ocen oraz planować działania tak, aby kapitał mógł pracować efektywnie przez długie lata. W efekcie inwestor staje się bardziej świadomy, spokojny i konsekwentny, a jego pieniądze zyskują realną szansę na wzrost zgodny z oczekiwaniami.
